Una fracción o quebrado es la división de algo en partes. Si tomamos como ejemplo la fracción 2/4 se lee como dos cuartos, y lo que hace es señalar dos partes sobre las cuatro partes totales. Podemos observar entonces que lo que da nombre a esta fracción es el número de abajo el cual llamamos denominador ya que “denominamos” a la fracción como dos “cuartos”. El número superior de una fracción, que es el que se divide por el denominador se llama denominador. Tanto el numerador como el denominador son siempre números enteros, por lo cual las cifras que representan las fracciones son números racionales.
Diremos que dos fracciones son heterogéneas cuando estas poseen distinto denominador, por lo cual se diferencian de las fracciones homogéneas, que tienen el denominador en común. Si lo que queremos es realizar sumas o restas con fracciones heterogéneas lo que debemos hacer en primer lugar, es encontrar el común denominador, o sea hallar el mínimo común múltiplo de todos los denominadores. Luego de esto lo que se debe hacer es colocar el denominador común, dividimos entonces el común denominador entre el primer denominador y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultados obtenidos y así finalizamos. A veces no es necesario multiplicar entre si los denominadores, eso depende de las fracciones que tengamos. Veamos ahora un ejemplo de suma de fracciones heterogéneas bastante sencillo:
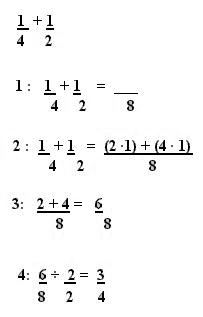
Vemos en el ejemplo anterior que en primer lugar se multiplicaron los denominadores, luego se realizó la multiplicación cruzada. Se sumaron los productos para obtener luego el numerador y finalmente se simplificó la fracción. Observemos otro ejemplo:
![]()
Podemos observar en este ejemplo que no fue necesario multiplicar entre si los denominadores, ya que 8 es múltiplo común tanto de 2 como de 4 así como de si mismo.
En la resta o sustracción de fracciones heterogéneas debemos utilizar las mismas reglas que usamos en la suma, lo único que cambia es que en este caso tenemos que restar en vez de sumar. Veamos un ejemplo:
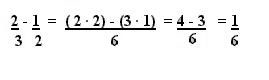
En la multiplicación de fracciones, tanto fracciones homogéneas como heterogéneas se multiplican de igual forma. El producto de dos o más fracciones es entonces igual a otra fracción que tiene como numerador el producto de los numeradores y tiene también como denominador el producto de los denominadores. Veamos un claro ejemplo:
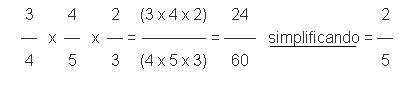
Dividamos fracciones heterogéneas o no, debemos cambiar siempre a una multiplicación y la segunda fracción cambiará entonces a su recíproco. El cociente de dos fracciones será otra fracción que tendrá como numerador el producto del numerador de la primera por el denominador de la segunda y tendrá por denominador el producto del denominador de la primera multiplicado por el denominador de la segunda.Veamos por último el siguiente ejemplo:
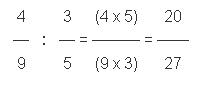
No hay comentarios:
Publicar un comentario